Earlier today I set you the following problem featuring Albert, Bernard and Cheryl, the protagonists in a viral puzzle from a decade ago. Here it is again with the solution.
Cheryl’s house number problem
Cheryl: I have thought of two distinct one-digit numbers. The last digit of the product of the two numbers is the last digit of Bernard’s house number. What is the sum of these two numbers?
Albert: I do not know what Bernard’s house number is.
Bernard: I know my house number, of course, and I know what the sum of the two numbers is.
Albert: At first, I did not know what the sum of the two numbers is, but now I know.
What is the sum of the two numbers?
Solution 10
Let Cheryl’s two numbers be a and b. Here is a table of possible values for the final digit of ab, with the possible pairs whose product has that final digit, and the possible sums a + b .
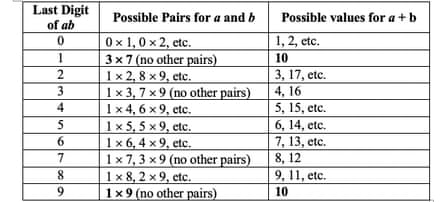
Say Bernard’s house number ends in 2. Cheryl may have thought of 1 and 2 (1 x 2 = 2), or 3 and 4 (3 x 4 = 12), or 8 and 9 (8 x 9 = 72). So the sum a + b could be 3, 7, 17 etc. Bernard cannot know with 100 per cent certainty the value of a + b.
The only time Bernard can know the sum is when there is only one possibility for a + b. If you look at the table, the only time a + b is unique is when the last digit is 1 or 9. In both cases, the sum is 10.
At the end of the process we do not know Cheryl’s numbers. We just know their sum.
I hope you enjoyed the puzzle – I’ll be back in two weeks.
If you want to see the solution for the Cheryl’s birthday problem, click here.
Thanks to Joseph Yeo for today’s puzzle.
I’ve been setting a puzzle here on alternate Mondays since 2015. I’m always on the look-out for great puzzles. If you would like to suggest one, email me.

 1 month ago
27
1 month ago
27













































